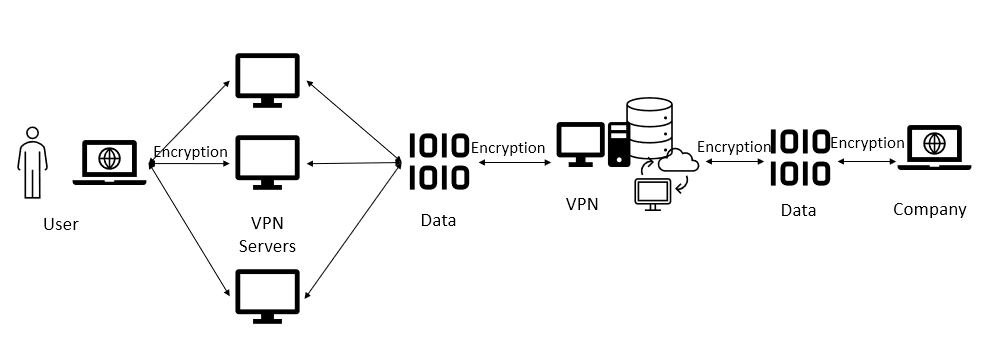
The art of encrypted communication evolved through the ages to safeguard data. From the earliest ciphers to the most sophisticated algorithms, cryptography is a key part of the digital infrastructure today. At the heart of this development is the use of primes and semi-prime numbers for encryption keys, allowing information to remain private from prying eyes. But even this powerful system is at risk because quantum computing is in the process of overturning the paradigm of security. Let’s take a very short look into this space.

A Brief History of Cryptography

The journey of cryptography began with simple substitution ciphers. One of the earliest examples is the Caesar cipher, where letters are shifted by a fixed number to obscure a message. The need for more complex encryption methods grew with the advancement of communication and warfare. By the 16th century, cryptographers developed polyalphabetic ciphers like the Vigenère cipher, which used multiple shifting patterns, making it much harder to crack.

And the 20th century saw the introduction of electro-mechanical encryption machines like the German Enigma machine during the Second World War. Its exploitation by Alan Turing and his Bletchley Park cryptographers showed the potential and finiteness of encryption. This was a new age that would demand mathematical encryption – one that could be cracked open by a capable adversary’s tools.

Prime and Semi-Prime Numbers in Encryption

Modern cryptography, in particular asymmetric encryption, rests on the mathematics of prime and semi-prime numbers. Prime numbers are numbers with one or more positive divisors of 1 and themselves. A semi-prime number consists of exactly two primes. Both these ideas have built the popular RSA encryption algorithm.

RSA Encryption: Prime and Semi-Prime Foundations

Developed in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, RSA encryption relies on the difficulty of factoring large semi-prime numbers. Here’s how it works at a high level:

1. Key Generation:
   • Two large prime numbers p  and q are selected.
   • Their product n=p×q becomes the modulus used in the encryption and decryption processes.
   • A public exponent e  and private exponent d are chosen such that they satisfy a mathematical relationship based on p and q.
2. Encryption:
   • The public key, composed of n and e, is shared openly.
   • A message M is encrypted using the formula:
     C=M^e  mod n, where C is the cyphertext
3. Decryption:
   • Using the private key (which includes d and n), the ciphertext can be decrypted with:
     M=C^d  Mod n.

RSA’s integrity rests on the fact that multiplying two large primes is computationally trivial, but factoring the semi-prime into its primes is impossibly complicated without knowing one of them in advance. The 2048-bit RSA key, for instance, has a semi-prime greater than 600 digits, and it is unusable for classic computers to brute-force its factors.

How Encryption Algorithms Leverage Mathematical Complexity

The hardness of mathematical problems is a key feature exploited in cryptography. In RSA, the prime factorization problem ensures security. Other algorithms rely on different mathematical challenges, such as:

• Elliptic Curve Cryptography (ECC): Uses the difficulty of solving elliptic curve discrete logarithm problems.
• Diffie-Hellman Key Exchange: Relies on the difficulty of computing discrete logarithms in modular arithmetic.
• Advanced Encryption Standard (AES): Though AES is symmetric encryption (not using primes), it operates on complex transformations involving mathematical matrices and substitutions.

In each case, the security of the algorithm depends on the problem’s resistance to computational solutions.

The Quantum Computing Threat

While these cryptographic systems are secure against classical computers, quantum computing introduces a new paradigm. Quantum computers leverage the principles of quantum mechanics to solve certain mathematical problems exponentially faster than classical machines. Two quantum algorithms pose specific threats:

1. Shor’s Algorithm: Can efficiently factor large semi-prime numbers, rendering RSA encryption vulnerable.
2. Grover’s Algorithm: While not as devastating, it speeds up brute-force attacks on symmetric encryption algorithms, such as AES.

If large, fault-tolerant quantum computers are built into reality, a good deal of existing encryption will go extinct. This has inspired the advent of post-quantum cryptography, protocols capable of countering attacks by quantum computers. NIST (National Institute of Standards and Technology) has begun standardizing post-quantum cryptographic algorithms that may become the replacement for RSA and ECC as the cornerstone of secure communication.

A New Era in Cryptography

This interaction of primes and semi-primes has been an engine of contemporary encryption, which provides secure digital communication worldwide. From the brilliant wits of pre-Internet ciphers to the mathematics of RSA and ECC, encryption was always ahead of attackers – until now.

Quantum computing poses a serious threat to the discipline and demands that cryptographers restructure encryption protocols. As we begin to explore the technology of post-quantum algorithms, companies need to adapt to this new age of protection. Just as cryptography has proven itself to meet every previous problem, it will adapt again to keep our most important data safe, even under the new quantum computer.

The race is fully on building quantum computers and implementing quantum-proof encryption. Its final result might define secure communication for generations to come.